Understanding Linear Regression
Understanding Linear Regression
Linear regression is such a common subject when learning data science, and it is a good starting point for most beginners to build a model. In general, most people use libraries like Tensorflow to get this done, but today we are going to understand step by step how does Linear Regression work. Dont get me wrong, this libraries are really useful. But doing it from scratch teaches us a lot more than we think (even if our linear regression performance is worse than the Tensorflow one). Lets dive into it now!
What is Linear Regression? Well, basically it is a linear approach for modelling the relationship between a scalar response and one or more explanatory variables. For today, we will only look into simple linear regression, that is, when we have only one explanatory variable (or independent).
The relationship is modeled using linear predictor functions, and model parameters are estimated from the data (which makes it a linear model).
Linear regression focuses on conditional probability distribution of the response given the values of predictors (given two jointly distributed random variables X and Y, conditional probability distribution of Y given X is the probability of Y when X is known its value).
Therefore, a a model using linear regression assumes that the relationship between dependent and independent variable is linear. We say there is a regression relationship between X and Y when the mean of Y varies with X.
A simple way to think about this is height and weight. Consider a relationship between height (Y) and weight (X) of a group of people. Lets say that the mean height at a given height is
p(x) = 3x / 5 - 38
for all x > 110.
The difference between an observed weight (real one) and mean weight at a given height provided by our formula is referred to as the error for that weight.
Therefore, we can said that the equation for linear regression is:
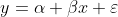
where y is (in our example) the height of some individual, alpha is some parameter (represented in this case by negative 38 minus error), beta is another parameter (represented by 3/5) and the error (minus 38 minus alpha).
That said, to discover our linear relationship, we could measure the height of three individuals at each weight and apply linear regression to model the mean height as a function of weight using a straight line. The most popular way to estimate parameters is the least-squares estimator (LSE). Before understanding this, remember your high school math classes. In this equation, beta is the slope of the line, and alpha plus error is the interception point. Now lets continue with LSE.
The method of least squares estimates the solution of our equations by minimizing the sum of the squares of the residuals (where the residual is the difference between observed value and fitted value provided by model) made in the results of each individual equation.
The estimates are given by:
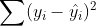
Where
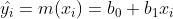
The above equation are the points on the estimated regression line (called the fitted ones, or predicted). The estimates are given by:
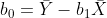
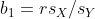
Where X and Y are means of samples x and y, and sx, sy are their standard deviation values, and r is their correlation coefficient.
LSE is really common because it is good for general error distributions, and this means that when we pick a random Y value from the conditional distribution Y|X, the LSEs will not be too high or too low (although they might deviate from the real values). However, this approach is sensitive to extreme values, or outliers from both sides. This means we have to clean outliers or evaluate them before applying LSE.
If you want to understand how this happens in code, I highly recommend taking a look on this repository:
GitHub - Lorenzobattistela/linear-regression
Here, I build a simple linear regression model from scratch, building all helpers and math functions needed for it to work. More instructions on how to run it on repository README.
Linear regression is a good way to start studying models and understanding the math behind it. It does not finish on simple LR, since we can have multivariable models. That said, that is a lot to explore and understand about it, and best part is that is easier to do by yourself!
Thanks for reading this article.
Best regards, Lorenzo.
References:
Altman, N., Krzywinski, M. Simple linear regression. Nat Methods 12, 999–1000 (2015).
https://en.wikipedia.org/wiki/Simple_linear_regression
https://en.wikipedia.org/wiki/Linear_regression